01 기체

기체의 성질
⑴ 기체의 압력과 부피
① 기체의 압력：기체 분자들은 자유롭게 운동하면서 기체가 담긴 용기의 벽에 충돌하여 힘을가하는데, 이로 인해 기체의 압력이 나타난다.
② 대기 압력의 측정：1643년 토리첼리는 수은을 채운 유리관을 이용하여 대기 압력을 측정하였다. 이때 해수면에서 측정한 수은 기둥 높이 760 mm에 해당하는 대기 압력을 1 atm이라고 한다.

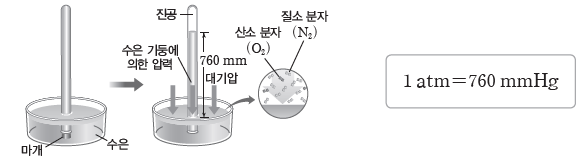③ 기체의 부피：기체 분자들이 운동하는 공간을 의미하며, 기체는 용기 전체로 퍼지는 성질이 있으므로 기체의 부피는 항상 기체가 들어 있는 용기의 부피와 같다. 또한, 2가지 이상의 기체가 한 용기에 들어 있을 때에도 각 기체의 부피는 용기의 부피와 같다.
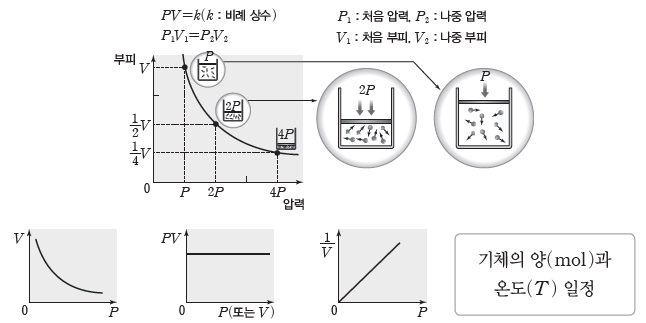
⑵ 보일 법칙：일정한 온도에서 일정량의 기체의 부피(V)는 압력(P)에 반비례한다. 즉, 일정한 온도에서 일정량의 기체의 압력과 부피의 곱은 항상 일정하다.

① 일상생활에서 보일 법칙 사례
• 자동차가 충돌할 때 팽창한 에어백은 사람과 부딪히면서 압력을 받게 되고 부피가 줄어들면서 사람에게 가해지는 충격이 완화된다.
• 물속에서 잠수부의 호흡으로 만들어진 기포는 수면에 가까워질수록 받는 압력이 감소하므로 기포의 부피가 점점 커진다.
• 하늘로 날린 풍선은 위로 올라가면서 대기 압력이 감소하므로 크기가 점점 커진다.
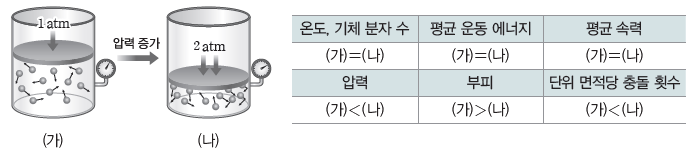
② 기체 분자 운동과 보일 법칙：일정한 온도에서 외부 압력을 2배로 하면 기체의 부피가 1/2배로 줄어든다. 따라서 단위 부피당 분자 수가 2배로 증가하여 단위 면적당 충돌 횟수도 2배로 증가한다. 충돌 횟수가 2배로 증가하면 단위 면적에 미치는 힘의 크기도 2배로 증가하므로 기체의 압력이 2배가 된다.

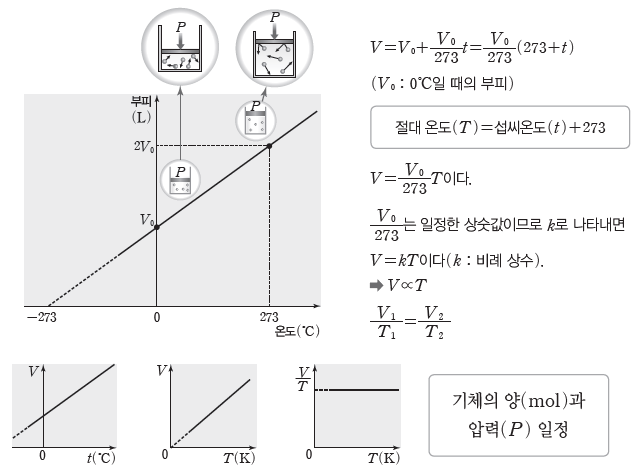
⑶ 샤를 법칙：일정한 압력에서 일정량의 기체의 부피(V)는 절대 온도(T)에 비례한다. 온도가 1℃ 높아질 때마다 0℃일 때 부피(V₀)의 1/273씩 증가한다.

① 일상생활에서 샤를 법칙 사례
•찌그러진 탁구공을 뜨거운 물에 넣으면 탁구공이 펴진다.
•자동차 타이어는 추운 겨울철이 여름철보다 부피가 줄어들어 공기를 더 주입한다.
•풍선을 액체 질소에 넣으면 쭈그러들고 꺼내면 다시 원래의 모양이 된다.
•열기구에 열을 가하면 기체의 부피가 팽창하여 밀도가 줄어들어 위로 뜬다.
② 기체 분자 운동과 샤를 법칙：일정한 압력에서 실린더 속에 들어 있는 기체의 온도를 높이면 기체 분자의 평균 운동 에너지가 증가하여 기체 분자가 더 빠르게 운동한다. 이때 실린더 내부 벽면에 충돌하는 기체 분자의 단위 시간당 충돌 횟수와 충돌의 세기가 증가하게 된다. 따라서 실린더 내부의 압력이 높아지고 실린더 내부의 압력(기체의 압력)과 외부 압력이 같아질 때까지 용기 내부의 부피가 증가하게 된다. 또한 이때 부피가 증가하여 일정하게 된 후의압력은 온도를 높이기 전의 압력과 같다.

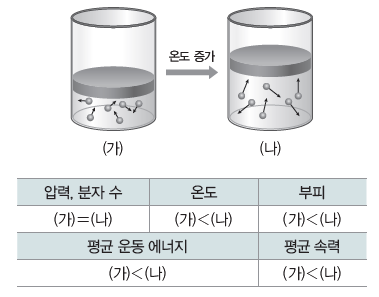(4) 보일·샤를 법칙：일정량의 기체에 대해 기체의 부피(V), 압력(P), 절대 온도(T) 사이의 관계를 정리한 것으로, 부피(V)는 압력(P)에 반비례하고, 절대 온도(T)에 비례한다.

⑸ 아보가드로 법칙：온도와 압력이 일정할 때 기체의 종류에 관계없이 같은 부피에 들어 있는 기체의 양(mol)은 같다.
① 일정한 온도와 압력에서 기체의 부피(V)는 기체의 종류에 관계없이 기체의 양(mol)에 비례한다.

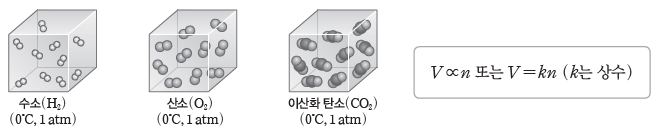② 기체 1 mol의 부피：0℃, 1 atm에서 기체 1 mol의 부피는 기체의 종류에 관계없이 22.4 L이다.
⑹ 이상 기체 방정식
기체의 압력(P)과 부피(V), 기체의 양(mol), 절대 온도(T) 사이의 관계를 나타낸 방정식이다.

① 이상 기체는 분자 간 인력 또는 반발력이 작용하지 않고, 기체 분자 자체의 부피를 무시할 수 있는 가상적인 기체이다.
② 기체의 분자량 측정：이상 기체 방정식을 이용하여 기체 분자의 분자량을 구할 수 있다.
⇨ 어떤 기체의 분자량을 M이라고 하면 기체의 양(mol) n=w/M (w：기체의 질량)이므로 다음과 같이 이상 기체 방정식을 이용하여 분자량을 구할 수 있다.

⑺ 기체 분자 운동론
기체 분자의 운동을 설명하기 위한 이론을 기체 분자 운동론이라고 하는데, 기체 분자 운동론은 다음과 같은 가정을 바탕에 두고 있으며, 이와 같은 특성을 가지는 기체를 이상 기체라고 한다.

① 보일 법칙과 기체 분자 운동론：온도가 일정할 때 기체 분자들의 평균 운동 속력은 일정하므로 기체가 들어 있는 실린더 내부 벽에 충돌할 때 일정한 압력을 유지한다. 이때 외부 압력을 증가시키면 다음과 같은 과정을 통해 기체의 부피가 감소한다.

② 샤를 법칙과 기체 분자 운동론：기체의 온도가 높아지면 기체 분자의 평균 운동 에너지가 증가하면서 기체 분자의 평균 운동 속력이 증가한다. 이때 기체가 들어 있는 실린더 내부 벽에 충돌하는 충돌 수 및 충돌의 세기가 증가하면서 내부 압력이 증가하고, 기체의 부피가 증가한다.

③ 아보가드로 법칙과 기체 분자 운동론：기체 분자의 양(mol)이 증가하면 다음과 같은 과정을 통해 기체의 부피가 증가한다.

혼합 기체와 부분 압력
⑴ 부분 압력 법칙
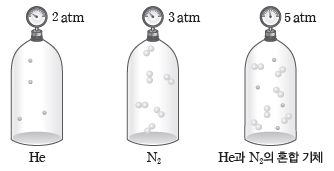
① 부분 압력과 전체 압력：서로 반응하지 않는 2가지 이상의 기체가 같은 용기 속에 혼합되어 있을 때, 각 성분 기체가 나타내는 압력을 각 성분 기체의 부분 압력이라고 하며, 혼합된 각 기체의 부분 압력의 합을 전체 압력이라고 한다.
예) 일정한 온도에서 같은 부피의 용기 속에 들어 있는 2 atm의 헬륨(He) 기체와 3 atm의 질소(N₂) 기체를 같은 부피의 동일한 용기에 함께 넣어 혼합하면 전체 압력은 5 atm이 된다.

② 부분 압력 법칙：일정한 온도 T에서 n_A만큼의 양(mol)의 기체 A를 부피가 V인 용기에 넣었을 때의 압력을 P_A라고 하고, n_B만큼의 양(mol)의 기체 B를 부피가 V인 용기에 넣었을 때의 압력을 P_B라고 하면, 이상 기체 방정식으로부터 다음과 같은 관계식이 성립한다.

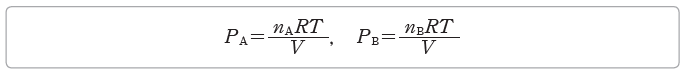
일정한 온도에서 서로 반응하지 않는 n_A만큼의 양(mol)의 기체 A와 n_B만큼의 양(mol)의 기체 B를 부피가 V인 용기에 함께 넣어 혼합하면 혼합 기체의 전체 압력 P_T는 전체 양(mol)인 n_A+n_B에 비례한다.

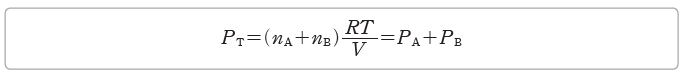따라서 P_T=P_A+P_B임을 알 수 있다. 1801년 돌턴은 혼합 기체의 전체 압력은 각 성분 기체의 부분 압력의 합과 같다는 사실을 밝혀냈고, 이것을 부분 압력 법칙이라고 한다.

⑵ 몰 분율
① 몰 분율：혼합 기체에서 각 성분 기체의 양(mol)을 전체 기체의 양(mol)으로 나눈 값을 그 기체의 몰 분율이라고 한다. 용기 속에 기체 A, B가 각각 n_A mol, n_B mol이 존재하면 각 기체의 몰 분율은 다음과 같다.

② 부분 압력과 몰 분율：혼합 기체에서 각 성분 기체의 부분 압력은 그 기체의 몰 분율에 비례하며, 다른 기체에 영향을 받지 않는다. 즉, 혼합 기체에서 각 성분 기체의 부분 압력은 전체 압력(P_T)에 그 기체의 몰 분율을 곱한 값과 같다.

참고자료: EBS 수능 특강 화학2