09 행성의 운동 (2)

행성의 공전 주기와 궤도 반지름

(1) 공전 주기

① 공전 주기: 행성이 태양 둘레를 한 바퀴 도는 데 걸리는 시간이다.

② 행성의 공전 주기 구하기: 지구는 다른 행성들과 함께 태양 둘레를 공전하고 있으므로 지구에서 직접 행성의 공전 주기를 측정하기 어렵다. 따라서 회합 주기를 이용하여 행성의 공전 주기를 구한다.

(2) 회합 주기

① 회합 주기: 내행성이 내합(또는 외합)에서 다음 내합(또는 외합)이 되는 데까지, 외행성이 충(또는 합)에서 다음 충(또는 합)이 되는 데까지 걸리는 시간이다.

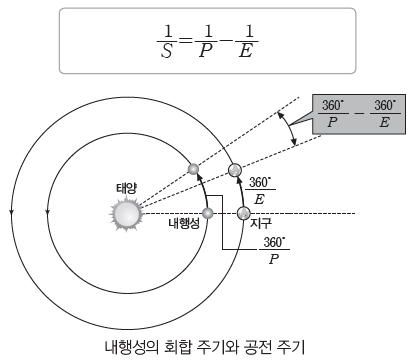
② 내행성의 회합 주기

• 내행성의 공전 주기를 P, 지구의 공전 주기를 E라고 할 때, 하루 동안 내행성과 지구가 공전한 각도는 각각 360°/P와 360°/E이다. 내합에서 동시에 공전을 시작했을 때 내행성은 지구보다 하루에 (360°/P-360°/E) 만큼씩 앞서게 된다. 이 각도 차가 누적되어 360°가 되면 내행성은 다시 내합에 위치하므로, 이 기간이 회합 주기(S)가 된다.

(360°/P-360°/E)×S=360°

• 내행성의 회합 주기(S)와 공전 주기(P) 사이에는 다음과 같은 관계가 성립한다.

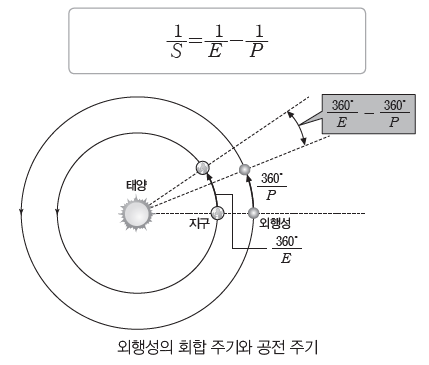
③ 외행성의 회합 주기

• 외행성의 공전 주기를 P, 지구의 공전 주기를 E라고 할 때, 하루 동안 외행성과 지구가 공전한 각도는 각각 360°/P와 360°/E이다. 충에서 동시에 공전을시작했을 때 지구는 외행성보다 하루에 (360°/E-360°/P) 만큼씩 앞서게 된다. 이 각도 차가 누적되어 360°가 되면 외행성은 다시 충에 위치하므로, 이 기간이 회합 주기(S)가 된다.

(360°/E-360°/P)×S=360°

• 외행성의 회합 주기(S)와 공전 주기(P) 사이에는 다음과 같은 관계가 성립한다.

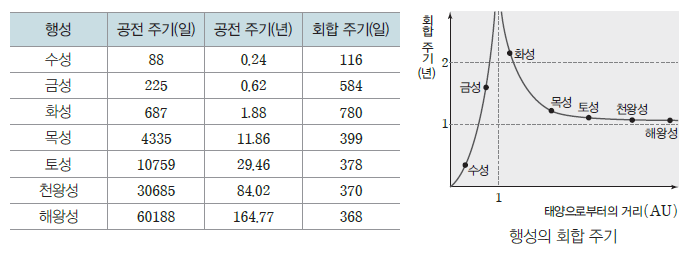
④ 행성의 거리와 회합 주기

• 내행성은 지구에 가까울수록 회합 주기가 길다. ⇨ 수성은 회합 주기가 1년보다 짧고, 금성은 1년보다 길다.
• 외행성은 지구에서 멀수록 회합 주기가 짧아지면서 점점 1년에 가까워진다. ⇨ 이는 지구로부터 거리가 먼 외행성일수록 지구가 태양 둘레를 1회 공전하는 동안 외행성이 공전하는 각이 작아지기 때문이다.
• 지구에서 관측한 어느 행성의 회합 주기와 그 행성에서 관측한 지구의 회합 주기는 같다.
• 두 행성의 공전 각속도 차가 클수록 회합 주기가 짧아진다.

(3) 행성의 공전 궤도 반지름

① 내행성의 공전 궤도 반지름: 내행성의 최대 이각을 이용하여 내행성의 공전 궤도 반지름을 구할 수 있다.

② 외행성의 공전 궤도 반지름: 지구에서 관측한 태양과 행성의 상대적 위치와 행성의 공전 주기를 이용하여 외행성의 공전 궤도 반지름을 구할 수 있다.

 

케플러 법칙

(1) 케플러 제1법칙-타원 궤도 법칙

① 행성은 태양을 한 초점으로 하는 타원 궤도를 공전한다.

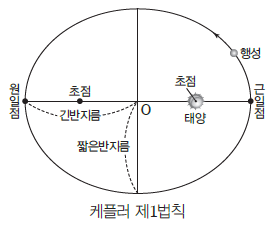
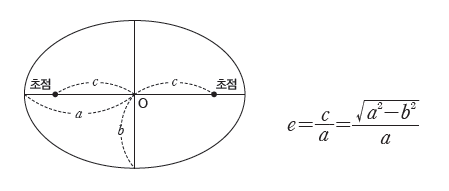
② 궤도 긴반지름: 타원 궤도의 중심으로부터 원일점 또는 근일점까지의 거리이다. 궤도 긴반지름은 태양과 행성 사이의 평균 거리에 해당한다.

③ 타원 궤도에서 태양에 가장 가까운 지점을 근일점, 가장 먼 지점을 원일점이라고 한다.

④ 궤도 이심률: 타원의 납작한 정도를 나타내는 값으로, 타원의 긴반지름에 대한 초점 거리의 비를 의미한다. 타원은 궤도 이심률이 클수록 더 납작한 모양이 되고, 이심률이 작을수록 원에 가까워지며, 이심률이 0이면 원이 된다.

• 타원의 긴반지름을 a, 짧은반지름을 b, 초점 거리를 c라고 할 때, 이심률(e)은 다음과 같이나타낸다.

(2) 케플러 제2법칙-면적 속도 일정 법칙

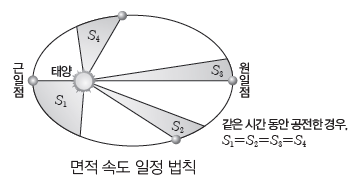
① 행성이 타원 궤도를 따라 공전할 때 태양과 행성을 잇는 선분은 같은 시간 동안 같은 면적을쓸고 지나간다.

② 행성의 공전 속도는 근일점에서 가장 빠르고, 원일점에서 가장 느리다.

③ 타원 궤도의 이심률이 클수록 근일점과 원일점에서의 공전 속도 차이가 커진다.

(3) 케플러 제3법칙-조화 법칙

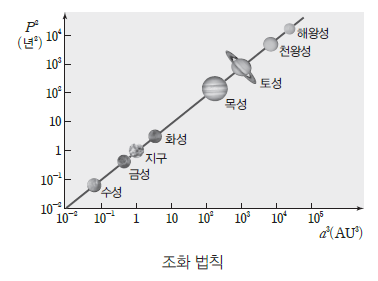
① 행성의 공전 주기의 제곱은 공전 궤도 긴반지름의 세제곱에 비례한다.

② 행성의 공전 주기 P와 행성의 공전 궤도 긴반지름 a 사이에는 다음과 같은 관계가 성립한다.

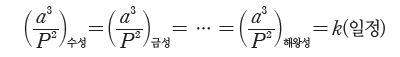
이때 P의 단위를 년, a의 단위를 AU로 하면, 비례 상수 k=1이 된다.

③ 행성의 회합 주기를 측정하여 공전 주기를 구하면 케플러 제3법칙을 이용하여 행성의 공전궤도 긴반지름을 구할 수 있다.

④ 공전 궤도 긴반지름이 큰 행성일수록 공전 속도가 느리다.

⇨ 수성의 공전 속도가 가장 빠르다.

(4) 케플러 제3법칙의 응용

① 쌍성을 이용한 케플러 제3법칙 유도

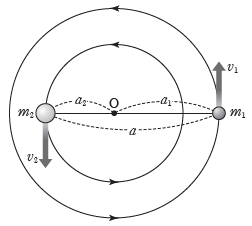
• 그림과 같이 질량이 각각 m₁, m₂인 두 천체가 공통 질량 중심 O로부터 a₁, a₂만큼 떨어진 거리에서 각각 v₁과 v₂의 속력으로 등속 원운동하고 있다. 두 천체의 공전 주기는 P이다. 두 천체의 등속 원운동에 필요한 구심력을 각각 F₁, F₂라고 할 때, F₁= (m₁v₁²)/a₁, F₂=m₂v₂²/a₂ 이다. v₁=(2πa₁)/P, v₂=(2πa₂)/P이므로 F₁=(4π²a₁m₁)/P², F₂=(4π²a₂m₂)/P²이다. 천체의 원운동을 일으키는 구심력은 두 천체 사이에 작용하는 만유인력인 F= (Gm₁m₂)/a²와 같으므로 F₁=F₂=F이다. 따라서 두 천체에 작용하는 힘은 아래와 같이 나타낼 수 있다.

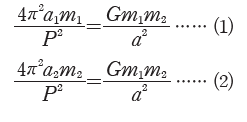
(1)과 (2)를 정리하면4π²(a₁+a₂)/P²=G(m₁+m₂)/a²이다. (a₁+a₂)=a이므로 a³/P²= G(m₁+m₂)/4π²가 성립한다.

• 이 공식을 태양계에 적용하면, 태양의 질량(M⊙)은 행성의 질량(m)에 비해 매우 크므로, 위의 식은 아래와 같이 나타낼 수 있다.

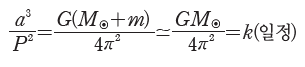
② 케플러 제3법칙의 응용

• 두 별 사이의 거리와 공전 주기를 알면 케플러 제3법칙으로부터 쌍성계의 질량을 구할 수 있고, 공통 질량 중심으로부터 별까지의 거리 비를 알면 별 각각의 질량도 결정할 수 있다.
• 공전 주기의 단위를 년, 거리의 단위를 AU로 나타내면 케플러 제3법칙으로부터 m₁+m₂= a³/P²·4π²/G이고, 4π²/G=1M⊙(M⊙: 태양 질량)이므로, 두 별의 질량의 합은 다음과 같이 구할 수 있다

• a₁m₁=a₂m₂의 관계가 성립하므로, a₁/a₂을 측정하면 별의 질량을 각각 구할 수 있다.

(5) 케플러 법칙의 적용

① 별과 은하 및 행성이 아니면서 태양 주위를 공전하는 소행성, 왜소 행성, 혜성 등도 케플러법칙에 따라 운동한다.

② 행성 주위를 공전하는 위성이나 지구 주위를 도는 인공위성도 케플러 법칙에 따라 운동한다.

③ 우주 탐사선을 발사할 때 연료의 소모를 최소로 하기 위해서 케플러 법칙을 이용하여 궤도를 결정하고 있다. ⇨ 행성 탐사선의 궤도는 지구를 근일점, 탐사하고자 하는 행성을 원일점에 둔 타원 궤도를 이용하는 것이 가장 경제적이다.

참고자료: EBS 수능 특강 지구과학2