운동량
(1) 운동량
① 같은 속력이라도 질량이 큰 물체는 멈추기가 어렵고, 같은 질량이라도 속력이 빠르면 멈추기가 어렵다. 이와 같이 물체가 운동하는 정도는 물체의 질량과 속력에 따라 다르다.
② 운동량(p): 물체의 운동하는 정도를 나타낸 물리량으로, 물체의 질량과 속도의 곱으로 나타낸다. 즉, 질량이 m, 속도가 v인 물체의 운동량 p는 다음과 같다.
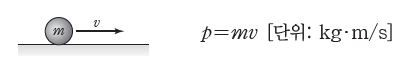
- 운동량의 방향은 속도의 방향과 같다.
- 운동량은 크기와 방향을 갖는 물리량으로, 직선상에서 두 물체가 서로 반대 방향으로 운동할 때 어느 한 방향에 (+)부호를 붙이면, 반대 방향에는 (-)부호를 붙인다.

(2) 운동량 변화량
① 물체에 힘이 작용하면 물체의 속도가 변하게 되어 물체의 운동량이 변한다.
② 운동량 변화량(Δp): 직선상에서 운동하는 물체의 운동량 변화량은 물체의 나중 운동량과 처음 운동량의 차이다. 즉, 질량이 m인 물체의 처음 속도가 v0, 나중 속도가 v일 때 물체의운동량 변화량 Δp는 다음과 같다.
Δp=mv–mv0 [단위: kg·m/s]
- 운동량 변화량의 방향은 물체에 작용하는 힘의 방향과 같다.
운동량 보존 법칙
(1) 운동량 보존 법칙
① 물체에 힘이 작용하지 않으면 물체의 속도가 변하지 않으므로 운동량도 변하지 않는다.
② 그림과 같이 수평면에서 질량이 각각 mA, mB이고 충돌 전 속도가 각각 vA, vB인 두 물체 A, B가 서로 충돌한 후 속도가 각각 vA‘, vB‘가 되었다.

- 충돌 전 A, B의 운동량의 합: mAvA+mBvB
- 충돌 후 A, B의 운동량의 합: mAvA‘+mBvB‘
- 충돌 순간, 작용 반작용 법칙에 따라 A, B는 서로 같은 크기의 힘(F)을 같은 시간(Δt) 동안 서로 반대 방향으로 받는다. 따라서 A, B에 뉴턴 운동 제2법칙을 적용하면 다음과 같다.
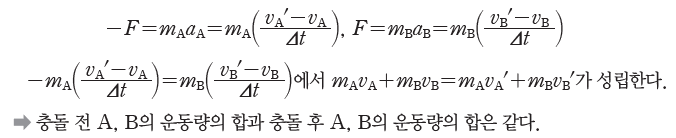
⇨ 충돌 전 A, B의 운동량의 합과 충돌 후 A, B의 운동량의 합은 같다.
③ 운동량 보존 법칙: 물체가 충돌할 때 외부에서 힘이 작용하지 않으면 충돌 전과 충돌 후 물체들의 운동량의 합은 일정하게 보존된다. 이것을 운동량 보존 법칙이라고 한다.
- 충돌하는 물체들의 운동량 변화량의 총합은 0이다. 즉, ΔpA+ΔpB=0이다.
- 운동량 보존 법칙은 상호 작용하는 힘의 종류나 물체의 크기에 관계없이 성립한다.
(2) 여러 가지 충돌
① 같은 방향으로 운동할 때의 충돌: 그림과 같이 같은 방향으로 운동하는 범퍼카 A, B가 서로 충돌하면, A는 운동 방향과 반대 방향으로 힘을 받게 되어 속력이 감소하고, B는 운동 방향과 같은 방향으로 힘을 받게 되어 속력이 증가한다(vA>vA‘, vB<vB‘).
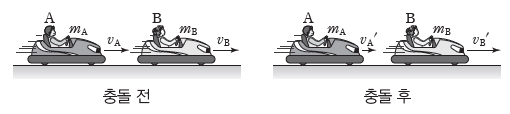
② 한 덩어리가 될 때의 충돌: 그림과 같이 두 물체 A, B가 충돌하여 충돌 후 한 덩어리가 되어 운동할 때, 운동량이 보존되므로 충돌 후 한 덩어리가 된 물체의 속력 v는 mAvA+mBvB=(mA+mB)v에서 v= (mAvA+mBvB)/(mA+mB)이다.
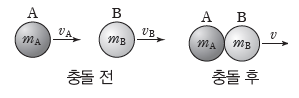
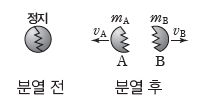
③ 한 물체가 두 물체로 분열될 때: 그림과 같이 분열 전 정지해 있던 물체가 두 물체 A, B로 분열될 때 운동량 보존 법칙이 성립한다. 분열 전 물체의 운동량이 0이므로 분열 후 A, B의 운동량의 합은 0이다. 0=mAvA+mBvB에서 mAvA=-mBvB이다. 즉, 분열 후 A, B의 운동량의 크기는 같고 방향은 서로 반대이다.
충격량
(1) 충격량
① 물체가 충돌할 때 물체에 작용하는 힘과 힘이 작용한 시간에 따라 운동량 변화량이 다르다.
② 충격량 ( I ): 물체가 충돌할 때 물체가 받는 충격의 정도를 나타낸 물리량으로, 물체에 작용하는 힘과 힘이 작용한 시간의 곱으로 나타낸다. 즉, 물체에 힘 F가 시간 Δt 동안 작용할 때 물체가 받는 충격량 I는 다음과 같다. 이때 충격량의 방향은 물체에 작용하는 힘의 방향과 같다.
I=FΔt [단위: N·s]
③ 힘–시간 그래프
- 힘의 크기가 일정할 때: 그림 (가)에서 그래프가 시간 축과 이루는 사각형의 면적은 Ft이므로 충격량을 나타낸다.
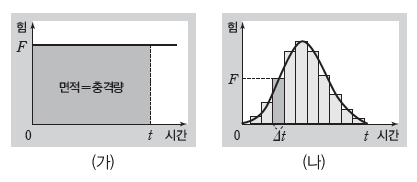
- 힘의 크기가 변할 때: 그림 (나)에서 짙게 색칠한 직사각형의 면적은 매우 짧은 시간 Δt 동안 받은 충격량과 같으므로, 직사각형들의 면적을 모두 더하면 그래프가 시간 축과 이루는 면적과 같아진다. 즉, 면적은 충격량과 같다.
2) 충격량과 운동량의 관계: 질량이 m인 물체에 일정한 힘 F가 시간 Δt 동안 작용하여 속도가 v0에서 v로 변할 때 뉴턴 운동 제2법칙을 적용하면, F=ma=m((v–v0)/Δt)= (mv–mv0)/Δt에서 FΔt=mv–mv0이므로 물체가 받은 충격량과 운동량 변화량의 관계는 다음과 같다.

① 운동량 변화량의 방향과 충격량의 방향은 모두 물체에 작용하는 힘의 방향과 같다.
② 힘의 단위 N은 kg·m/s2이므로, 충격량의 단위 N·s는 운동량의 단위 kg·m/s와 같다.
(3) 충격량과 힘의 관계: I=FΔt ⇨ F= I/Δt =Δp/Δt
① 힘이 일정하면 힘을 받는 시간이 길수록 충격량의 크기가 크다.
I∝Δt (F: 일정)
② 힘을 작용하는 시간이 일정하면 힘의 크기가 클수록 충격량의 크기가 크다.
I∝F (Δt: 일정)
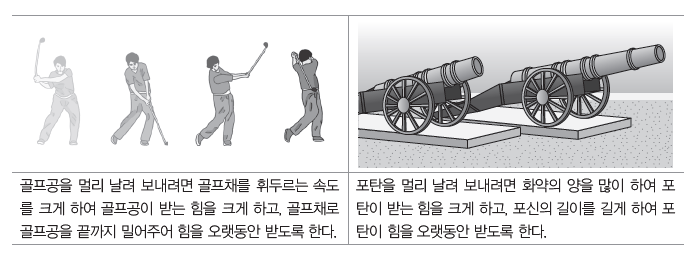
(4) 충돌과 안전장치
① 충격력: 물체가 충돌할 때 받는 힘을 충격력이라고 한다.
② 충격력과 시간의 관계: 물체가 받는 충격량이 일정할 때 힘을 받는 시간이 길수록 물체에 작용하는 충격력의 크기는 작다. ⇨ F∝ 1/Δt ( I: 일정 )
③ 충격력 줄이기
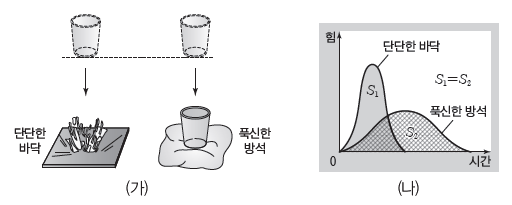
- 그림 (가)의 왼쪽은 유리잔이 단단한 바닥에, 오른쪽은 푹신한 방석에 떨어지는 경우를 나타낸 것으로, 유리잔이 받는 충격량은 같지만 단단한 바닥에 떨어진 유리잔은 깨졌고, 푹신한 방석에 떨어진 유리잔은 깨지지 않았다. 그림 (나)는 유리잔이 충돌하는 동안에 받는 힘을 시간에 따라 나타낸 것으로, 그래프가 시간 축과 이루는 면적은 같지만 푹신한 방석에 떨어진 경우가 충돌 시간이 길어 유리잔이 받는 평균 힘의 크기가 작다. 이와 같이 충돌할 때 충돌 시간을 길게 하면 충격력의 크기가 작아진다.
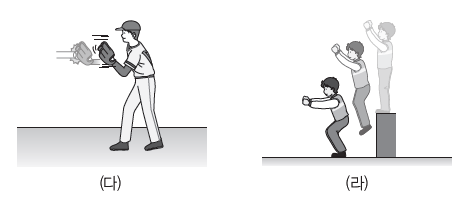
- 그림 (다)와 같이 날아오는 야구공을 받을 때 글러브를 뒤로 빼면서 받으면 충격력을 감소시킬 수 있다.
- 그림 (라)와 같이 높은 곳에서 뛰어내릴 때 무릎을 살짝 굽히면 충격력을 감소시킬 수 있다.
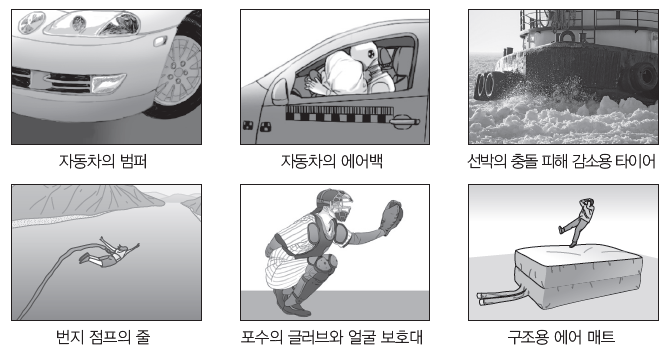
④ 여러 가지 안전장치: 일상생활에서 충돌할 때 충돌 시간을 길게 하여 충격력을 감소시킨다.
예) 자동차의 범퍼, 자동차의 에어백, 선박의 충돌 피해 감소용 타이어, 번지 점프의 줄, 포수의 글러브와 얼굴 보호대, 구조용 에어 매트 등
참고자료: EBS 수능 특강 물리1