힘의 합성과 분해
(1) 스칼라량과 벡터량
① 스칼라량: 길이, 질량, 시간, 이동 거리, 속력, 에너지 등과 같이 크기만으로 표시할 수 있는 물리량을 스칼라(scalar)량이라고 한다.
② 벡터량: 1차원 직선이나 2차원 평면이나 3차원 공간에서의 운동을 표시하기 위해서는 크기와 방향을 함께 표시해야 한다. 이와 같이 크기뿐만 아니라 방향을 함께 나타내는 물리량을 벡터(vector)량이라고 한다.
- 벡터량의 예: 변위, 속도, 가속도, 힘, 운동량 등
- 벡터량의 표시: 벡터량을 표시할 때에는 일반적으로 A와 같이 굵은 글씨로 나타내거나, A와 같이 문자 위에 화살표를 붙여서 나타낸다.
- 벡터량의 크기: A의 크기는 |A|와 같이 절댓값으로 나타내거나 A와 같이 화살표를 쓰지 않고 나타낸다.
(2) 벡터의 합성: 둘 이상의 벡터를 같은 효과를 갖는 하나의 벡터로 나타내는 것을 벡터의 합성이라고 한다.
① 평행사변형법: 두 벡터 A와 B를 이웃한 두 변으로 하는 평행사변형을 그리면, 평행사변형의 대각선 C가 벡터의 합이 된다. 즉, 합성 벡터의 방향은 대각선의 방향과 같고, 크기는 대각선의 길이와 같다.
② 삼각형법: B의 시작점을 A의 끝점으로 평행 이동시키면, A의 시작점과 B의 끝점을 연결한 화살표 C가 벡터의 합이 된다.
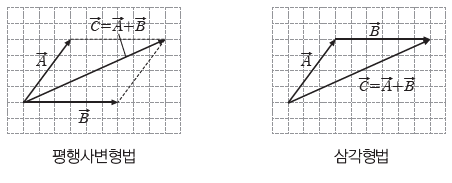
③ 여러 벡터의 합성: 세 개 이상의 벡터를 합성하는 경우에는 두 벡터를 합성하는 방법을 반복하여 벡터의 합을 구한다.
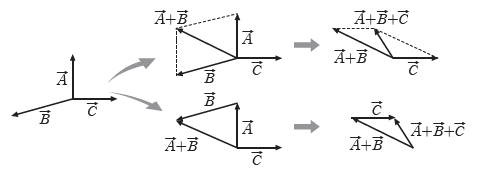
④ 벡터의 차: A에서 B를 빼는 것은 A에 -B를 더하는 것과 같다.
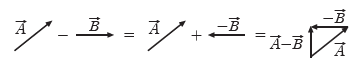
(3) 벡터의 분해: 벡터의 합성과는 반대로 한 개의 벡터를 두 개 이상의 벡터로 나누는 것을 벡터의 분해라고 한다.

돌림힘
(1) 돌림힘: 물체의 회전 운동을 변화시키는 원인을 돌림힘 또는 토크라고 한다.
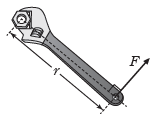
① 돌림힘의 크기: 회전 팔의 길이를 r, 회전 팔에 수직으로 작용한 힘의 크기를 F라고 하면, 돌림힘의 크기 τ는 다음과 같다.

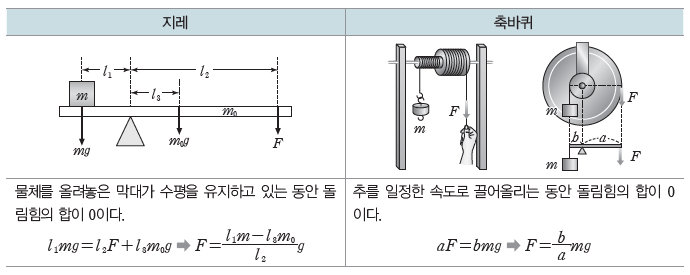
② 지레와 축바퀴: 지레나 축바퀴를 이용하면 작은 힘으로 무거운 물체를 들 수 있다.
물체의 평형
(1) 평형 상태: 물체에 작용하는 힘들이 평형 조건을 만족하면, 물체가 평형 상태에 있다고 한다.
① 평형 조건
- 힘의 평형: 물체에 작용하는 알짜힘이 0이다.
- 돌림힘의 평형: 물체에 작용하는 돌림힘의 합이 0이다.
② 평형 상태에서 가능한 운동: 정지, 등속 직선 운동
(2) 무게중심: 물체를 구성하는 입자들의 평균 위치 개념 체크
① 균일한 물질로 이루어진 공이나 정육면체의 무게중심은 중앙에 있다.
② 무게중심을 받치면 물체 전체를 떠받칠 수 있다.
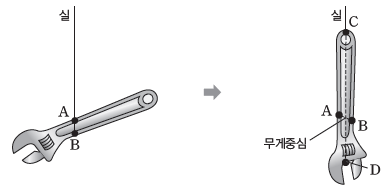
③ 무게중심 찾기: 물체의 가장자리를 실에 매달면 무게중심은 실의 연장선에 있다. 따라서 AB와 CD가 만나는 점이 무게중심이다.
(3) 구조물의 안정성
① 구조물이 안정적으로 정지해 있기 위한 조건: 구조물이 안정한 평형 상태에 있어야 한다.
② 구조물의 안정성: 바닥이 넓고 무게중심이 낮을수록 구조물의 안정성이 높다.
③ 실생활에서 구조물의 안정성
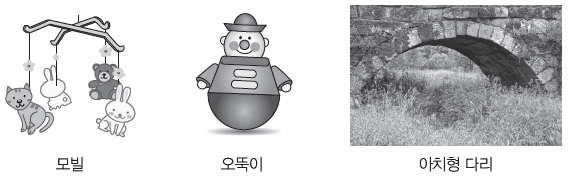
- 모빌이나 오뚝이는 안정한 평형 상태에 있다. 따라서 한쪽으로 기울였다 놓으면 흔들리다가 처음과 같은 평형 상태로 되돌아온다.
- 아치형 다리는 위에서 누르는 힘을 아치를 이루는 돌들에 잘 분산시키며, 힘이 작용할수록아치를 이루는 돌들이 강하게 끼게 되어 안정성이 증가한다.
참고자료: EBS 수능 특강 물리2