일
(1) 일: 물체의 이동 방향과 나란하게 작용한 힘의 크기와 물체가 이동한 거리를 곱한 값을 힘이 물체에 한 일이라고 한다.
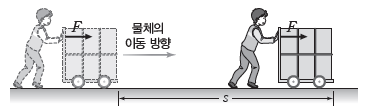
① 힘의 방향과 이동 방향이 같을 때: 힘이 물체에 한 일(W)은 힘의 크기(F)와 이동 거리(s)를 곱한 값과 같다.
⇨ W=Fs [단위: N·m=J(줄)]
② 힘의 방향과 이동 방향이 이루는 각이 θ일 때: 힘 F를 이동 방향과 나란한 성분 Fx와 수직인 성분 Fy로 분해한다.
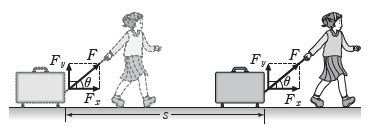
- Fy 방향으로 이동한 거리가 0이므로 Fy가 물체에 한 일은 0이다.
- 힘 F가 물체에 한 일은 Fx가 물체에 한 일과 같으므로 W=Fxs이다.
- Fx=Fcosθ이므로 힘 F가 물체에 한 일은 W=Fscosθ 이다.
(2) 힘–이동 거리 그래프와 일: 물체에 작용한 힘의 방향과 물체의 이동 방향이 같을 때, 힘–이동 거리 그래프에서 그래프가 이동 거리 축과 이루는 면적은 힘이 물체에 한 일과 같다.
① 힘의 크기가 일정할 때: 그림 (가)에서 그래프가 이동 거리 축과 이루는 사각형의 면적 Fs는 힘이 물체에 한 일을 나타낸다.
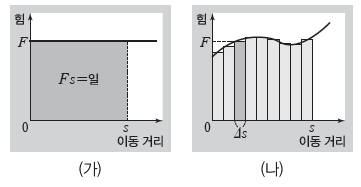
② 힘의 크기가 변할 때: 그림 (나)에서 짙게 색칠한 직사각형의 면적은 물체가 Δs만큼 이동할 때 힘이 물체에 한 일과 같다. 이때 직사각형의 면적을 모두 더하면 그래프가 이동 거리 축과 이루는 면적과 같으며, 이 면적은 s만큼 이동하는 동안 힘이 물체에 한 일을 나타낸다.
일과 에너지
(1) 운동 에너지(kinetic energy, Ek): 운동하는 물체가 가진 에너지로, 단위는 일의 단위와 같은 J(줄)을 사용한다.
① 질량이 m인 물체가 v의 속력으로 운동할 때(운동량의 크기 p=mv), 물체의 운동 에너지는 Ek=1/2mv2= p2/2m [단위: J]이다.
② 일·운동 에너지 정리: 물체에 작용하는 알짜힘이 한 일은 물체의 운동 에너지 변화량과 같다. 수평면상에서 속력이 v0이고 질량이 m인 수레에 운동 방향으로 일정한 힘 F를 작용하여 거리 s만큼 운동시켰을 때 수레의 속력이 v라면 F가 수레에 한 일 W는 다음과 같다.
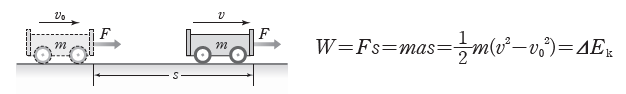
- 알짜힘이 수레에 한 일이 (+)인 경우(W>0): 수레의 운동 에너지 증가
- 알짜힘이 수레에 한 일이 (-)인 경우(W<0): 수레의 운동 에너지 감소
- 알짜힘이 수레에 한 일이 0인 경우(W=0): 수레의 운동 에너지 일정
(2) 퍼텐셜 에너지(potential energy, Ep): 중력, 탄성력, 전기력 등이 작용하는 계에서 물체 또는 계에 저장되는 에너지로, 기준점에서 어떤 지점까지 물체를 등속으로 이동시키는 데 필요한 일을 그 지점에서의 퍼텐셜 에너지라고 한다.
(3) 중력 퍼텐셜 에너지: 중력장에서 기준점(Ep=0)으로부터 물체를 어떤 지점까지 등속으로 이동시킬 때 작용한 힘이 물체에 한 일을 그 지점에서의 중력 퍼텐셜 에너지라고 한다. 물체를 기준점으로부터 높이 h까지 일정한 속력으로 들어 올리는 동안 힘 F가 물체에 한 일은 W=Fs=mgh이다. 따라서 기준점으로부터 높이 h인 곳에서 물체의 중력 퍼텐셜 에너지는 Ep=mgh [단위: J]이다.
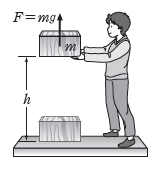
① 기준점이 달라지면 물체의 중력 퍼텐셜 에너지도 달라진다.
② 두 지점 사이에서 물체의 중력 퍼텐셜 에너지 차는 기준점에 관계없이 일정하다.
③ 기준점보다 낮은 위치에서는 물체의 중력 퍼텐셜 에너지가 (-)값을 갖는다.
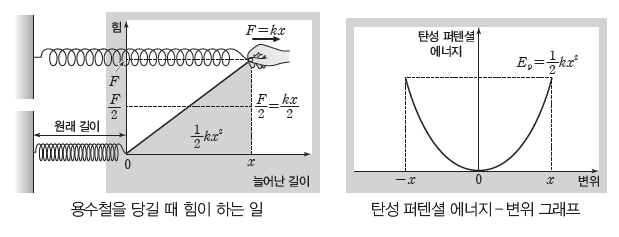
(4) 탄성 퍼텐셜 에너지(탄성력에 의한 퍼텐셜 에너지): 용수철과 같은 탄성체가 변형되었을 때 가지는 에너지이다. 용수철을 당기는 동안 힘은 일정하게 증가하며(F=kx, k: 용수철 상수), 평형 위치로부터 x만큼 당기는 동안 힘이 한 일 W는 힘–늘어난 길이 그래프의 아래 삼각형의 면적과 같으므로 W=1/2Fx=1/2kx2 이다. 즉, 힘 F가 용수철에 한 일은 1/2kx2 이므로, 평형 위치로부터 x만큼 늘어난 곳에서 탄성 퍼텐셜 에너지는 Ep=1/2kx2 [단위: J]이다.
역학적 에너지 보존
(1) 역학적 에너지: 물체의 운동 에너지와 퍼텐셜 에너지의 합을 역학적 에너지라고 한다.
(2) 중력에 의한 역학적 에너지 보존
① 중력 이외의 힘(마찰력, 공기 저항력 등)이 일을 하지 않으면 물체의 역학적 에너지는 일정하게 보존된다. ⇨ Ek+Ep=일정
- 물체의 운동 에너지 변화량과 물체의 중력 퍼텐셜 에너지 변화량의 합은 0이다.
- 물체의 운동 에너지가 증가하면 그만큼 물체의 중력 퍼텐셜 에너지는 감소하고, 물체의 운동 에너지가 감소하면 그만큼 물체의 중력 퍼텐셜 에너지는 증가한다.
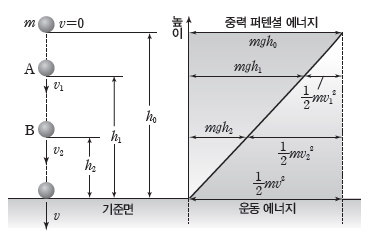
② 질량이 m인 물체가 자유 낙하 하면서 지면으로부터의 높이가 h1, h2인 두 지점 A, B를 지날 때의 속력을 각각 v1, v2라고 하면, 물체가 A에서 B까지 낙하하는 동안 중력이 물체에한 일은 W=Fs=mg(h1–h2)이고, 중력이 물체에 한 일과 물체의 운동 에너지 증가량이 같으므로 mg(h1–h2)=1/2mv22-1/2mv12이다.
이 식을 정리하면 mgh1+1/2mv12 = mgh2+1/2mv22 이므로, A와 B에서의 역학적 에너지는 같다.
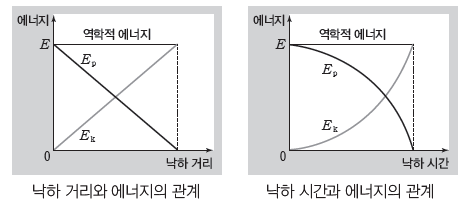
③ 자유 낙하 하는 물체의 에너지 전환 그래프: 물체가 자유 낙하 할 때 물체의 중력 퍼텐셜 에너지는 감소하고 물체의 운동 에너지는 증가하지만, 물체의 중력 퍼텐셜 에너지와 물체의 운동 에너지의 합인 물체의 역학적 에너지는 일정하다.
(3) 탄성력에 의한 역학적 에너지 보존
① 탄성력 이외의 힘(마찰력, 공기 저항력 등)이 일을 하지 않으면 물체의 운동 에너지와 탄성퍼텐셜 에너지의 합은 일정하게 보존된다. ⇨ Ek+Ep=일정
② 마찰과 공기 저항이 없을 때, 물체를 용수철에 연결하여 A만큼 당겼다가 놓으면 물체는 평형 위치 O를 중심으로 진폭이 A인 진동을 한다. 평형 위치에 가까워지면 물체의 운동 에너지가 증가하고 탄성 퍼텐셜 에너지는 감소하며, 평형 위치에서 멀어지면 물체의 운동 에너지가 감소하고 탄성 퍼텐셜 에너지는 증가한다.
그림에서 평형 위치 O로부터의 위치가 각각 x1, x2인 두 지점 P, Q를 지날 때 물체의 속력을 각각 v1, v2라고 하면, P에서 Q까지 이동하는 동안 탄성력이 한 일은 W=1/2kx12-1/2kx22 이다. 탄성력이 한 일이 물체의 운동 에너지 증가량과 같으므로 1/2kx12-1/2kx22=1/2mv22-1/2mv12이며, 이 식을 정리하면 1/2kx12+1/2mv12=1/2kx22+1/2mv22이다. 따라서 P와 Q에서 물체의 역학적 에너지는 같다. 진폭이 A이고 평형 위치에서의 속력이 V이면 물체의 역학적 에너지는 다음과 같다.
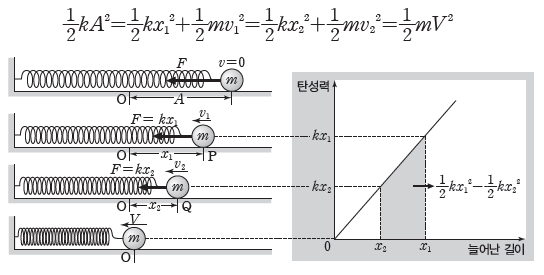
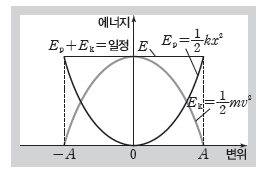
③ 용수철에서의 에너지 전환 그래프: 마찰과 공기 저항이 없을 때, 용수철에 연결된 물체가 진동하는 경우 탄성 퍼텐셜 에너지가 증가하면 물체의 운동 에너지는 감소하고, 탄성 퍼텐셜 에너지가 감소하면 물체의 운동 에너지가 증가한다. 그러나 탄성 퍼텐셜 에너지와 물체의 운동 에너지를 합한 역학적 에너지는 일정하다.
(4) 역학적 에너지 보존 법칙
① 마찰력, 공기 저항력 등과 같은 힘이 일을 하지 않으면 물체의 운동 에너지와 퍼텐셜 에너지의 합인 역학적 에너지는 일정하게 보존되는데, 이를 역학적 에너지 보존 법칙이라고 한다.
⇨ Ek+Ep=일정
② 역학적 에너지가 보존되는 경우에 물체의 운동 에너지가 증가하면 그만큼 퍼텐셜 에너지가감소하고, 물체의 운동 에너지가 감소하면 그만큼 퍼텐셜 에너지가 증가한다.
(5) 역학적 에너지가 보존되지 않는 경우: 마찰력, 공기 저항력 등과 같은 힘이 일을 하면 물체의 역학적 에너지는 열, 소리, 빛 등과 같은 다른 에너지로 전환되어 물체의 역학적 에너지는 감소하게 된다. 그러나 에너지는 새로 생성되거나 소멸하지 않으므로 전환 전의 에너지의 총량과 전환 후의 에너지의 총량은 같다.
참고자료: EBS 수능 특강 물리1